儒略日的用途及其轉換

我們現在所使用的以西元年、月、日表示的格里曆（Gregorian calendar），就像是把日期折疊起來表示的曆法。對我們平常的認知來說，這是很自然的，但因它不像十進位數那麼規律和單純，在做一些計算時很不方便，尤其在作不同曆法之間的轉換時更是麻煩。

法國學者 Joseph Justus Scaliger（1540-1609）設計了一種曆法，稱為”儒略日”(Julian day)。以JD表示。它是以7980年為一週期，我們所在的這一週期是以西元前4713年(或-4712年)1月1日12時為起點，在這週期內，每一個數就對應唯一的一個日，就像是把一般的日曆拉成一直線，完全以天數來計日，如此在計算上十分方便，

例如，我們若要知道2000年1月1日為星期幾，則可先求出這一日的儒略日為2451545（此即自西元前4713年1月1日12時起至2000年1月1日12時止之日數）。若西元前4713年1月1日為星期一，則求出（2451545+1）除以7的餘數為6，即為星期六。當餘數為0時代表星期天。

同樣的，在求算中國的日天干與日地支時亦是如此，若西元前4713年1月1日的天干為”癸”，這是天干中的第十個，若以第一個對應0，第二個對應1，第三個對應2，依此類推至第十個應對應9，所以求出（2451545+9）除以10的餘數為4，即”戊”之對應。

若西元前4713年1月1日的地支為”丒”，這是地支中的第二個，若以第一個對應0，第二個對應1，第三個對應2，依此類推至第十二個應對應11，所以求出（2451545+1）除以12的餘數為6，即”午”之對應。

要將格里曆日期轉換為儒略日，可有許多不同的方法或公式。底下即為一種方法。若以y代表年份，m代表月份，d代表月中日期,ut代表時(若含分、秒，可先化為小數的時，再加上整數的時)。int() 為程式中常用的取整數函數（在javascript中以Math.floor()替代）。mod 為取餘數之函數（在javascript中以%替代），x mod y就表示取x除以y的餘數。計算原則是以3月為一年之首月，2月為一年之末月，使2月29日成為四年的最後一日。如果我們以3月為一年中的第一個月，2月為前一年的末月，則經變數變換：

將1、2月歸為前一年

將3~12月對應到0~9月，將1~2月對應到10~11月

下式為將格里曆轉換為儒略日的公式,適用於1582年10月15日及以後：

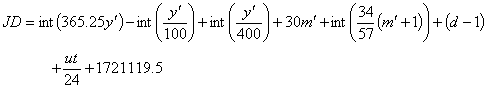
格里曆是在西元1582年10月15日開始使用的，在這之前使用的是儒略曆（與儒略日不同，不要混淆了），這是在西元前46年，由羅馬帝國的愷撒大帝所制訂。它只設定每隔四年的2月為閏月，所以平年為365日，閏年為366日。平均每年為365.25日。但平均回歸年為365.24219日，與365.25日差了約0.00781日，1500年後就差了11.7日。1582年，羅馬教皇格里高利十三世對儒略曆進行修改，在原有的基礎上規定百年不閏，四百年又閏。稱為格里曆，自1582年10月4日的次日開始使用。但為了減少先前儒略曆所造成的日數誤差，10月4日的次日直接跳到15日。

下式為將儒略曆轉換為儒略日的公式,適用于西元元年至1582年10月4日及以前：

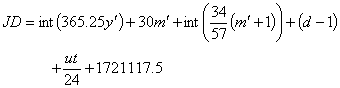
轉換的方法並非唯一，讀者亦可試著自行設計一個轉換副程式或函式。

反過來，儒略日轉換為格里曆或儒略曆，也是以1582年的10月15日0時為分界點。在這之前為儒略曆，之後為格里曆。通常與它的JD值2299160.5日比較。

轉換的方法亦可有多種，請直接參考程式原始檔中的函式Jtime()。