用橢圓軌道公式求出24節氣

以春分點為起點，可在軌道上每隔15度取一個點，將軌道劃分為24個區，這24個區就是24節氣。由軌道圖(此圖將偏心率誇大以方便觀察)中可看出每一節氣的路徑長是不同的。

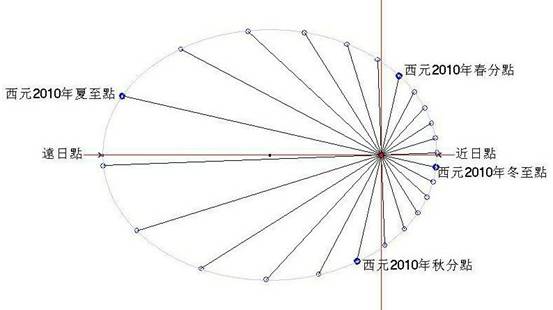
自刻卜勒所繪出的地球軌道可明顯地看出,當地球與太陽最接近時其運動速度最快.下面的圖中顯示地球軌道的(經誇大的)二極端部份。

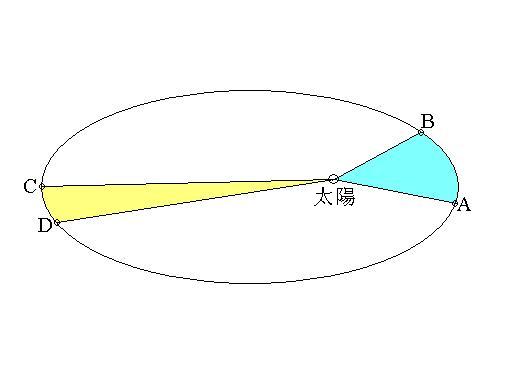
在軌道上相鄰二點間所歷之時間是相等的,因此,自A到B所歷之時間與自C到D所歷者相等.因為自A到B的距離較大,所以在這一段距離內,地球之運動速度較快;自C到D的距離較小, 所以在這一段距離內,地球之運動速度較慢.不過,刻卜勒看出:這二段不等的距離對太陽所展的面積卻是相等的.這使得刻卜勒相信:行星在沿著其軌道而運動時,它與太陽的連線在相等的時間內所掃過的面積相等.此即刻卜勒第二定律(Kepler's second law),也稱為面積定律(law of areas).

由面積定律可知，地球在繞日的軌道上，單位時間內掃過的面積是固定值，因此，在不同節氣內，地球的運行速度是不同的，在近日點附近的速度較快，在遠日點附近的速度較慢。

在方程式

中r是θ之函數,.然而,在節氣的計算上,所需要的函數不是r(θ),而是t (θ),我們希望得到一個公式,給予θ(真實近點角),為一時間t之函數,式中只包含兩個基本的軌道觀察常數作為參數,即週期τ和偏心率ε.我們可以以下列方法來作這個計算.因為它需要物體徑向量掃過整個橢圓軌道面積所花費的時間τ,且因為運動面積速度是一常數,因此在一個時間t內,其掃過之面積為

我們可以將此表示式改寫為一面積之積分式

根據面積微分方程式

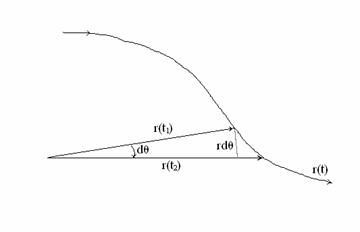
若我們在t=0時取θ= 0,則

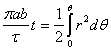
將方程式

代入，則

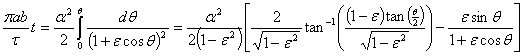
上式中利用到解微分方程的公式：

當 時，掃過的面積正好是橢圓的上半部，此時

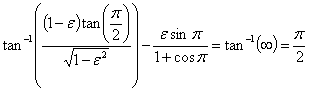
原式可簡化為

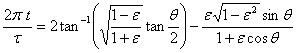
將此式寫為一以θ為變數的函數t(θ)

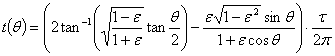
我們可用Jean Meeus提供的公式求出指定年春分點的JD值。

用前一節中得到的公式求出指定年春分點的近點角δ

將δ值加上15°，30°，45°，60°…等，因爲这些數據是度度量，須乘以 轉換為弳度量，然后代入上面的t(θ)公式，可分別求出清明點、穀雨點、立夏點、小滿點…等各節氣點與近日點的日數差。再分別將這些值減去春分點與近日點的日數差即得各節氣點與春分點的日數差。分別將這些日數差加上春分點的JD值，即得各節氣點的JD值。

請參看程式中的函式MeanJQJD()。