實際的新月點
首先要決定的是新月的時刻與朔望月的長度。由於每個朔望月的長度並非固定,以目前這個年代來說,朔望月的週期平均值約為29日 12時 30分,各朔望月與此平均值之差是以一種複合波的型式變化,如下圖所示,橫軸代表自2000年1月6日起的朔望月序數,縱軸代表各朔望月長與平均朔望月長的差值,單位為小時。在後面我們對這圖的形成會有較詳細的分析。
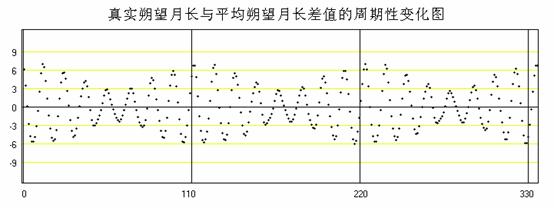
前一節我們已經求出了指定時刻附近的新月序數,此為一整數。
k’=INT((jd-2451550.09765)/msm)
k=k’+phase
phase代表月相,其值為0,0.25,0.5,0.75時分別對應新月、上弦月、滿月、下弦月。本章討論新月,故phase為0。
k代入下式可求出其所對應的均值新月點JD值
mnm=bnm+msm×k+adj
利用k和mnm這兩個參數,代入下面的一些公式,就可以求出實際的新月點。
實際的新月點tnm為均值新月點mnm加上因攝動而產生的調整值,如下式所示:
tnm=mnm+p1+p2
![]()
|
i |
Xi |
Yi |
Zi |
|
1 |
-0.40720 |
1 |
m’ |
|
2 |
0.17241 |
e |
m |
|
3 |
0.01608 |
1 |
|
|
4 |
0.01039 |
1 |
|
|
5 |
0.00739 |
e |
m’-m |
|
6 |
-0.00514 |
e |
m’+m |
|
7 |
0.00208 |
e2 |
|
|
8 |
-0.00111 |
1 |
m’ |
|
9 |
-0.00057 |
1 |
m’+ |
|
10 |
0.00056 |
e |
|
|
11 |
-0.00042 |
1 |
|
|
12 |
0.00042 |
e |
m+ |
|
13 |
0.00038 |
e |
m |
|
14 |
-0.00024 |
e |
|
|
15 |
-0.00017 |
1 |
Ω |
|
16 |
-0.00007 |
1 |
m’+ |
|
17 |
0.00004 |
1 |
|
|
18 |
0.00004 |
1 |
|
|
19 |
0.00003 |
1 |
m’+m |
|
20 |
0.00003 |
1 |
|
|
21 |
-0.00003 |
1 |
m’+m+ |
|
22 |
0.00003 |
1 |
m’-m+ |
|
23 |
-0.00002 |
1 |
m’-m |
|
24 |
-0.00002 |
1 |
|
|
25 |
0.00002 |
1 |
|
![]()
|
i |
Bi |
Ai |
|
1 |
0.000325 |
299.77+0.107408k-0.009173t2 |
|
2 |
0.000165 |
251.88+0.016321k |
|
3 |
0.000164 |
251.83+26.651886k |
|
4 |
0.000126 |
349.42+36.412478k |
|
5 |
0.000110 |
84.66+18.206239k |
|
6 |
0.000062 |
141.74+53.303771k |
|
7 |
0.000060 |
207.14+2.453732k |
|
8 |
0.000056 |
154.84+7.306860k |
|
9 |
0.000047 |
34.52+27.261239k |
|
10 |
0.000042 |
207.19+0.121824k |
|
11 |
0.000040 |
291.34+1.844379k |
|
12 |
0.000037 |
161.72+24.198154k |
|
13 |
0.000035 |
239.56+25.513099k |
|
14 |
0.000023 |
331.55+3.592518k |
其中m為地球繞太陽運行的均值近點角(Sun’s mean anomaly)
![]()
m'為月球繞地球運行的均值近點角(Moon’s mean anomaly)
![]()
f為月球的緯度參數(Moon’s argument of latitude)
![]()
Ω為月球繞日運行軌道升交點之經度
![]()
![]()
e為一個調整乘數(此非偏心率)
![]()
包含參數m的項,因其與地球繞日運行軌道的偏心率相依,而此偏心率目前是隨時間的推移而減少,故這些項的振幅實際上是變數而非常數。若要將此影響列入考慮,則包含m或-m的項要乘上e,包含2m的項要乘上e2。
在這個調整式中,影響力最大的就是m和m’這兩個參數,以及包含這兩個參數的項:
-0.40720 sin(m’), 0.17241 e sin(m)
由於近點月的週期為27.55454988日,較朔望月的週期29.530588853日為短,故以近地點的座標來看朔望月,運轉的角度較大,在m’式中可看出,一個朔望月的時間,在近地點座標上看,運轉角度為385.81693528度,比一周多出了25.81693528度(385.81693528-360),14個朔望月之後,就多出了361.43709392度,也就是多轉了一圈,所以14個朔望月大約與15個近點月同步。
在一個朔望月的時間內,包含近地點附近時間區域的多寡,影響了朔望月的長短。若朔日發生在遠地點附近,則因包含兩次遠地點,月球平均速度較慢,故朔望月長較長。若朔日發生在近地點附近,則因包含兩次近地點,月球平均速度較快,故朔望月長較短。這樣的變化形成了一個波形,其週期就是14個朔望月或15個近點月,如下圖所示。
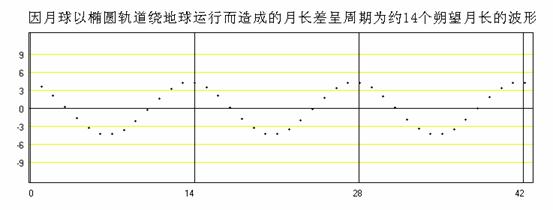
在m式中,一個朔望月的時間內,地球對太陽的近點角只增加了29.10535669度,約12.368857個朔望月才轉360度,也就是一年,而在地球繞日的橢圓軌道上,連續兩個朔日的張角都不同,當朔日發生在近日點附近時,因地球速度較快,故太陽對連續兩次合朔之月球與地球張角較大,故朔望月長較長。當朔日發生在遠日點附近時,因地球速度較慢,故太陽對連續兩次合朔之月球與地球張角較小,故朔望月長較短。這樣的變化形成了一個波形,其週期即為地球繞日運行的近點年,亦即大約12.368857個朔望月的時間。如下圖所示。
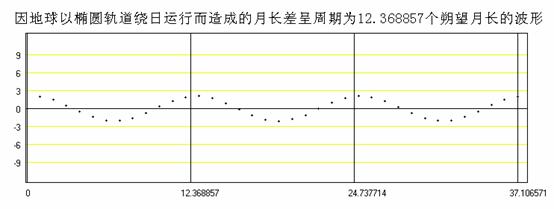
上面兩種不同週期的波合在一起,就會形成一個波包,這個波包的週期應為
![]()
即109.475個朔望月。這個週期也就是月球繞地球軌道的近地點對地球繞日軌道近日點前進360度所需要的時間。
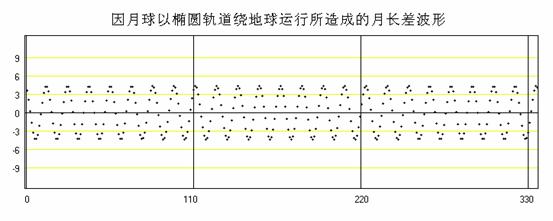
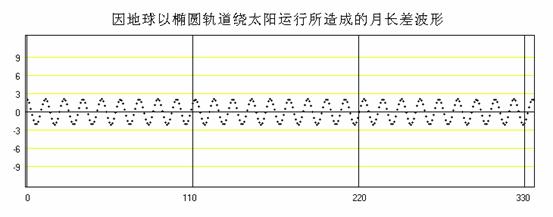
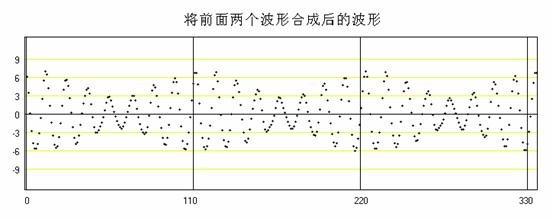
由圖中看到的最大正波峰表示當朔日發生於地球在近日點附近,且月球在遠地點附近時,朔望月長度為最長。最大負波峰表示當朔日發生於地球在遠日點附近,且月球在近地點附近時,朔望月長度為最短。