日蝕
日蝕與月蝕雖然與曆法及八字沒什麼關係，但歷史上的確有許多的重大事件，在記錄時輔以日蝕或月蝕的發生以為標記。中國大陸的學者江曉原先生就曾以史書春秋谷梁傳記載孔子出生前不久有日蝕發生來判定孔子的生日是在西元前552年8月22日而非西元前551年。
日蝕的情況較複雜，因日蝕的現象在地球上不同位置的觀察者所看到的都不一樣。但對於月蝕，地球上所有觀察者可同時見到同一現象。
程式算出來的日蝕，只能表示出日蝕的路徑是否經過地球，以及是否有全蝕，全環蝕，環蝕或偏蝕的發生，但無法指出哪些區域在這路徑內，哪些區域在這路徑外。譬如程式可算出2009年7月22日10時35分32秒，中國的北半球可看到日全蝕，但中國北半球的哪些區域會涵蓋在這日全蝕的路徑內則無法得知。且不同觀測點，日蝕發生的時間也不同，上述的時刻是以太平洋上的某點為觀測點，但在同一時刻，中國武漢觀測點看到的日全蝕卻早已結束了。
。有興趣的讀者可能需要涉獵一些專業天文書籍，作更精確的計算。
日蝕一定發生在新月點附近，月蝕一定發生在滿月點附近。因此首先就要求算均值新月點的序數k。
k=k’+phase
phase代表月相，phase為0、0.25、0.5、0.75時分別代表新月、上弦月、滿月、下弦月。
月相點的估計值(moon phase estimated)為
mpe=bnm+msm×k
估計的世紀變數值
調整值
jde=mpe+adj
當phase=0時，jde為均值新月點JD值
當phase=0.5時，jde為均值滿月點JD值
下列參數與第九章同，在此重列。
m為地球繞太陽運行的均值近點角(Sun’s mean anomaly)
m'為月球繞地球運行的均值近點角(Moon’s mean anomaly)
f為月球的緯度參數(Moon’s argument of latitude)
Ω為月球繞日運行軌道升交點之經度
e為一個調整乘數(此非偏心率)
下面的一些式子則都與第九章的不同，有兩個參數必須先求出：
最大日月蝕時間(time of maximum eclipse)
|
i |
Xi |
Yi |
Zi |
|
1 |
-0.4075(日蝕用) -0.4065(月蝕月) |
1 |
m’ |
|
2 |
0.1721(日蝕用) 0.1727(月蝕用) |
e |
m |
|
3 |
0.0161 |
1 |
2m’ |
|
4 |
-0.0097 |
1 |
2f1 |
|
5 |
0.0073 |
e |
m’-m |
|
6 |
-0.0050 |
e |
m’+m |
|
7 |
-0.0023 |
1 |
m’-2f1 |
|
8 |
0.0021 |
e |
2m |
|
9 |
0.0012 |
1 |
m’+2f1 |
|
10 |
0.0006 |
e |
2m’+m |
|
11 |
-0.0004 |
1 |
3m’ |
|
12 |
-0.0003 |
e |
m+2f1 |
|
13 |
0.0003 |
1 |
a1 |
|
14 |
-0.0002 |
e |
m-2f1 |
|
15 |
-0.0002 |
e |
2m’-m |
|
16 |
-0.0002 |
1 |
Ω |
另求參數p
|
i |
Ai |
Bi |
Ci |
|
1 |
0.2070 |
e |
m |
|
2 |
0.0024 |
e |
2m |
|
3 |
-0.0392 |
1 |
m’ |
|
4 |
0.0116 |
1 |
2m’ |
|
5 |
-0.0073 |
e |
m’+m |
|
6 |
0.0067 |
e |
m’-m |
|
7 |
0.0118 |
1 |
2f1 |
求參數q
|
i |
D |
Ei |
Fi |
|
1 |
-0.0048 |
e |
m |
|
2 |
0.0020 |
e |
2m |
|
3 |
-0.3299 |
1 |
m’ |
|
4 |
-0.0060 |
e |
m’+m |
|
5 |
0.0041 |
e |
m’-m |
求參數w
求參數γ
求參數u
|
i |
G |
Hi |
Ii |
|
1 |
0.0046 |
e |
m |
|
2 |
-0.0182 |
1 |
m’ |
|
3 |
0.0004 |
1 |
2m’ |
|
4 |
-0.0005 |
1 |
m’+m |
對日蝕的分析：
當日蝕發生時，γ代表月球陰影的軸心到地球中心的最短距離，以地球赤道的半徑為單位。
γ值的正負取決於月球錐形陰影的軸線是通過地球中心的北部或南部。
當γ值介於0.9972與-0.9972之間時，這日蝕是中央蝕(可能是全蝕或環蝕)，此時會有一條中央蝕帶於地球表面。
u代表月球本影錐或偽本影錐在基本平面上的半徑，0.5461為月球半影錐在基本平面上投影的內外圓間距離，同樣的都是以地球赤道的半徑為單位。(基本平面是經過地球中心且與月球陰影軸垂直的平面)請參考下圖。
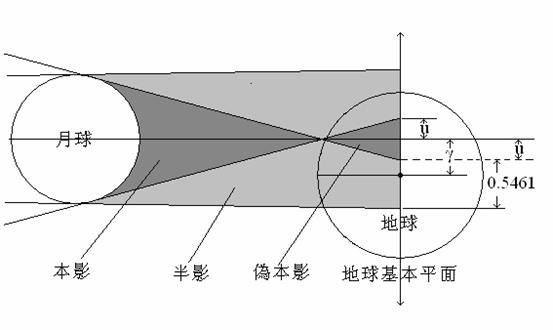
半影錐在基本平面的半徑是u+0.5461，上圖中是在偽本影區，u為正值，所以可寫為
。若是在本影區，則應寫為
。
若γ的絕對值是介於0.9972+|u| 和0.9972+0.5461之間，則這日蝕就不是中央蝕。大部份的這種情況都是日偏蝕。如下圖所示。
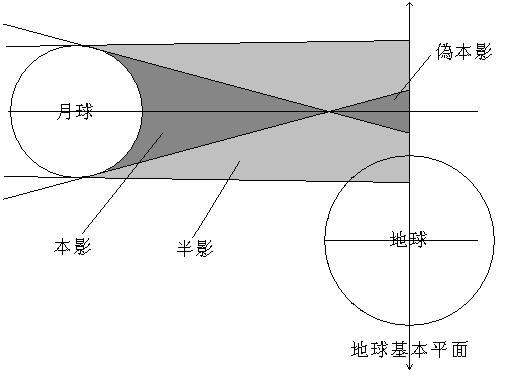
當γ的絕對值是介於.9972和1.0260之間，則月球本影錐的一部份可能會觸及到地球極區的表面。當
時，這些非中央蝕的全蝕或環蝕就會發生，如下圖所示。
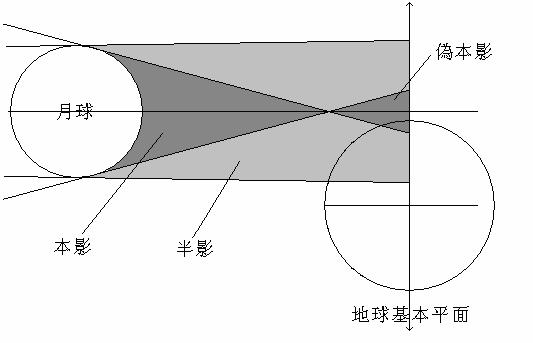
若
，則在地球上看不到日蝕，如下圖所示。
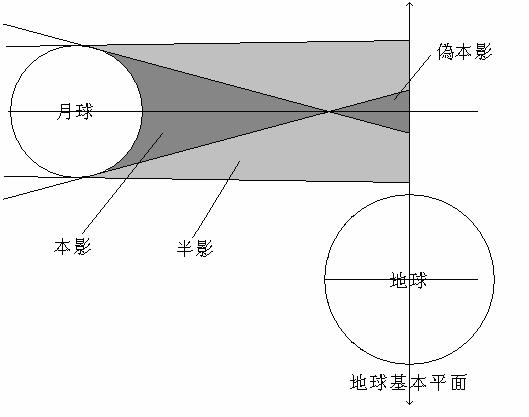
在中央蝕的情況下，日蝕的型態可由下列的規則決定：
若u<0，則為日全蝕。
若u>0.0047，則為日環蝕。
若u介於0與0.0047之間，則可能是日環蝕，也可能是全環蝕，這種不明的狀況是因為u所代表的是月球本影錐或偽本影錐在地球基本平面上的半徑，而非在地球表面上的。此時月球本影錐的頂點是介於地球基本平面和與地球最高點相切的平面之間。若錐形頂點落在地球表面下方，則有日全蝕，但在這之前和之後有部份時間錐形頂點不會落到地球上，此時為日環蝕，故其路徑為環蝕、全蝕、環蝕的蝕帶。若錐形頂點都在地球表面上方，則只有日環蝕。參考下圖。
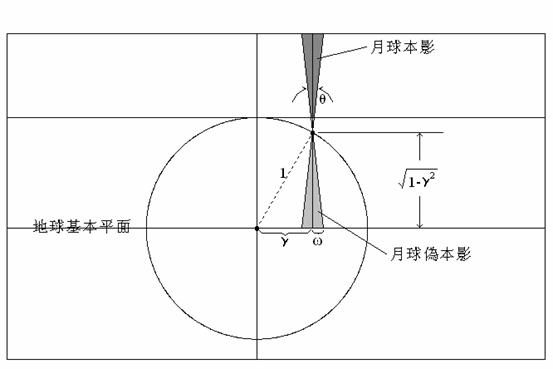
當錐形頂點在地表面時，可求出
此時u=ω，但當錐形頂點移至地表下時，u<ω，則此日蝕為全環蝕，當錐形頂點往上移離地表時，u>ω，則為日環蝕。
在日偏蝕的情況下，地球表面上最接近月球陰影的軸的地點，其蝕分的大小是最大的。在這個地點看到的日蝕大小為：
